Author Archive

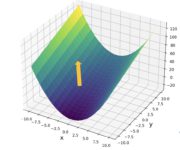
We learn how to construct and apply a matrix of partial derivatives known as the Jacobian matrix. In the process, we also introduce vector calculus. The Jacobian matrix is a matrix containing the first-order partial derivatives of a function. It gives us the slope of the function along multiple dimensions. Previously, we’ve discussed how

We learn how to take partial derivatives and develop an intuitive understanding of them by calculating the change in volume of a cylinder. Lastly, we explore total derivatives. Up until now, we’ve always differentiated functions with respect to one variable. Many real-life problems in areas such as physics, mechanical engineering, data science, etc., can

In this post, we are going to explain the product rule, the chain rule, and the quotient rule for calculating derivatives. We derive each rule and demonstrate it with an example. The product rule allows us to differentiate a function that includes the multiplication of two or more variables. The quotient rule enables us

In this post, we learn how to find the derivative of a function from first principles and how to apply the power rule, the sum rule, and the difference rule. We previously established that the definition of a derivative equals the following expression. Note that f'(x) is a more compact form to denote the

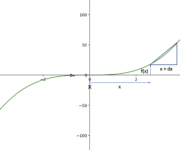
We introduce the basics of calculus by understanding the concept of rise over run, followed by a more formal definition of derivatives. At the heart of calculus are functions that describe changes in variables. In complex systems, we usually deal with many changing variables that depend on each other. The concept of rise over

In this post, we build an understanding of the singular value decomposition (SVD) to decompose a matrix into constituent parts. What is the Singular Value Decomposition? The singular value decomposition (SVD) is a way to decompose a matrix into constituent parts. It is a more general form of the eigendecomposition. While the eigendecomposition is

This series of blog posts aims to introduce and explain the most important mathematical concepts from linear algebra for machine learning. If you understand the contents of this series, you have all the linear algebra you’ll need to understand deep neural networks and statistical machine learning algorithms on a technical level. Most of my

In this post, we learn how to decompose a matrix into its eigenvalues and eigenvectors. We also discuss the uses of the Eigendecomposition. The eigenvalue decomposition or eigendecomposition is the process of decomposing a matrix into its eigenvectors and eigenvalues. We can also transform a matrix into an Eigenbasis (the basis matrix where every

In this post, we explain the concept of eigenvectors and eigenvalues by going through an example. What are Eigenvectors and Eigenvalues An eigenvector of a matrix A is a vector v that may change its length but not its direction when a matrix transformation is applied. In other words, applying a matrix transformation to

The Gram Schmidt process is used to transform a set of linearly independent vectors into a set of orthonormal vectors forming an orthonormal basis. It allows us to check whether vectors in a set are linearly independent. In this post, we understand how the Gram Schmidt process works and learn how to use it